Mecânica Quântica /

Conceitos fundamentais /
Teoria Quântica de Campos

A Teoria Quântica de Campos é a aplicação conjunta da Mecânica Quântica e da relatividade aos campos que fornece uma estrutura teórica usada na física de partículas e na física da matéria condensada. Em particular, a teoria quântica do campo eletromagnético, conhecida como eletrodinâmica quântica (tradicionalmente abreviada como QED, do inglês “Quantum EletroDynamics”), é a teoria provada experimentalmente com maior precisão na Física. Resumidamente, pode-se dizer que a teoria quantica dos campos é uma teoria que, na denominação mais antiga, se chama segunda quantização, isto é, realiza a quantização dos campos, ao passo que a Mecânica Quântica apenas realiza a quantização da matéria. A teoria quântica dos campos considera tanto a matéria (hadrons e leptons) quanto os condutores de força (bosons mensageiros) como excitações de um campo fundamental de energia mínima não-nula (vácuo).

História

Advento da teoria clássica dos campos

A noção de campo surgiu inicialmente como um constructo matemático “conveniente” para descrever as forças, que são conceitos centrais na mecânica de Newton. Entretanto, no século XIX, devido principalmente aos trabalhos de Maxwell, o conceito de campo passa a ocupar o papel central na descrição física da realidade. De fato, a mudança foi ainda maior, porque foi então que surgiu a primeira grande unificação da física: a identidade dos campos elétrico e magnético, bem como o reconhecimento de que a óptica é um capítulo do eletromagnetismo.

Mecânica, Eletromagnetismo e Relatividade

O eletromagnetismo foi a “raison d’être” do surgimento da relatividade. Com a inadequação das transformações de Galileu quando aplicadas à equação de onda tridimensional, surgiu um dilema. Ou se preservava a mecânica clássica e abandonava-se o nascente eletromagnetismo, ou se preservava este e abandonava-se quase três séculos de previsões bem confirmadas. O caminho foi achado, surpreendemente, numa espécie de conciliação entre as duas alternativas. Inicialmente, Voldemar Voigt, em 1887, derivou um conjunto de relações, baseado apenas na equação de onda ordinária, devida a Jean D’Alembert. Essas relações eram transformações espaciais e temporais que deixavam invariante a “forma” desta equação. Estas relações são as que se conhecem como transformações de Loretz-Fitzgerald, cientistas que redescobriram estas transformações mais tarde. Em particular, Lorentz o fez num contexto diferente, na tentativa de se reconciliar as teorias do éter com os resultados de experiências físicas, tais como a de Michelson-Morley. Einstein então entra em cena, com seu trabalho seminal de 1905, “Sobre a Eletrodinâmica dos Corpos em Movimento”, onde introduz a relatividade, interpretando corretamente as transformações de Lorentz-Fitzgerald como alterações do espaço e do tempo em função da velocidade relativa entre os referenciais.

Termodinâmica e Mecânica Quântica

A Mecânica Quântica surgiu da incapacidade conjunta da termodinâmica clássica e do eletromagnetismo para prever a correta distribuição de energias em função da frequência. A derivação tentativa feita por Lord Rayleigh e por James Jeans postulava que cada onda eletromagnética estava em equilíbrio com as paredes do forno. Isso se traduz num teorema que mantém sua validade mesmo na Mecânica Quântica:

Numa cavidade fechada em equilíbrio térmico com o campo eletromagnético confinado, o campo é equivalente a um conjunto enumeravelmente infinito de osciladores harmônicos e a sua energia é igual à soma das energias desses osciladores. Cada frequência corresponde aos osciladores tomados dois a dois.

Max Planck obteve a forma correta da distribuição porque postulou a quantização da energia dos osciladores harmônicos que comporiam as paredes da cavidade que confina a radiação. Essa hipótese teve por efeito introduzir um limite máximo de frequência acima do qual há um corte (cutoff) nas contribuições dos entes (ondas eletromagnéticas) que estão em equilíbrio. Einstein, para explicar o efeito fotoelétrico, ampliou o conceito da quantização para a energia radiante, postulando a existência do fóton (o que “implicitamente” quer dizer que as equações de Maxwell não tem validade ilimitada, porque a existência do fóton implica em não-linearidades). A antiga teoria quântica cedeu lugar à Mecânica Quântica moderna quando Schröndinger desenvolveu a famosa equação que leva o seu nome. Entretanto, a primeira versão que ele desenvolveu foi a equação que hoje é conhecida como equação de Klein-Gordon, que é uma equação relativista, mas que não descrevia bem o átomo de hidrogênio, por razões que só mais tarde puderam se entender. Assim, ele abandonou a primeira tentativa, chegando à sua equação (equação de Schrondinger):

$i\hbar\frac{\partial\Psi\left(\bold{r},t\right)}{\partial t} = [- \frac{\hbar^2\nabla^2}{2m} + V\left(\bold{r},t\right)]\Psi\left(\bold{r},t\right)$

A equação de Schröndinger acima colocada é a equação “dependente do tempo”, pois o tempo aparece explicitamente. Neste caso, as soluções Ψ são funções das coordenadas espaciais e do tempo. Quando o potencial V não depende do tempo, ou seja, quando o campo de força ao qual a partícula está submetida é conservativo, é possível separar as variáveis 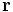$\bold{r}$ e t. A equação que a parte espacial da função de onda Ψ obedece é:

$[- \frac{\hbar^2\nabla^2}{2m}+V\left(\bold{r}\right)]\psi\left(\bold{r}\right)= E\psi\left(\bold{r}\right)$

conhecida como equação de Schrödinger “independente do tempo”. Esta é uma equação de autovalores, ou seja, através dela se obtem simultaneamente autofunções (no caso as funções de onda ψ) e autovalores (no caso, o conjunto das energias estacionárias E).

Primeiras unificações - Equações relativísticas

Equação de Klein-Gordon

Como foi dito acima, quando Schrondinger primeiro procurou uma equação que regesse os sistemas quanticos, pautou sua busca admitindo uma aproximação relativista, encontrando a depois redescoberta equação de Klein-Gordon:

$[\square + (\frac{mc}{\hbar})^2]\psi = 0$

onde

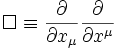
$\square \equiv \frac{\partial}{\partial x_\mu} \frac{\partial}{\partial x^\mu}$

A equação de Klein-Gordon, às vezes chamada de equação de Klein-Fock-Gordon (ou ainda Klein-Gordon-Fock) pode ser deduzida de algumas maneiras diferentes. Usando-se a definição relativística de energia

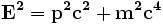
$\mathbf{E^2} = \mathbf{p^2c^2} + \mathbf{m^2c^4}$

chega-se à equação:

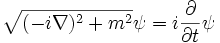
$\sqrt{(-i\mathbf{\nabla})^2 + m^2} \psi= i \frac{\partial}{\partial t}\psi$

Essa expressão, por conter operadores diferenciais sob o radical, além de apresentar dificuldades computacionais, também apresenta dificuldades conceituais, já que se torna uma teoria não-local (pelo fato de a raiz poder ser expressa como uma série infinita. Por ser uma equação de segunda ordem não permite que fique bem definida a questão da normalização da função de onda. Fock deduziu-a através da generalização da equação de Schrondinger para campos magnéticos (onde as forças dependem da velocidade). Fock e Klein usaram ambos o método de Kaluza e Klein para deduzi-la. O motivo, só mais tarde entendido, da inadequação desta equação ao átomo de hidrogênio é que ela se aplica bem somente a partículas sem carga e de spin nulo.

Equação de Dirac

Em 1928 Dirac obteve uma equação relativística baseada em dois princípios básicos

A equação deveria ser linear na derivada temporal A equação deveria ser relativisticamente covariante

A equação obtida por ele tinha a seguinte forma:

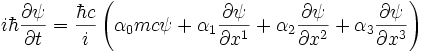
$i\hbar \frac{\partial \psi}{\partial t} = \frac{\hbar c}{i} \left(\alpha_0 mc\psi + \alpha_1 \frac{\partial\psi}{\partial x^1} + \alpha_2 \frac{\partial\psi}{\partial x^2} + \alpha_3 \frac{\partial\psi}{\partial x^3} \right)$

onde α₁, α₂, α₃ e β não são números reais ou complexos, mas sim matrizes quadradas com N² componentes. Semelhantemente, as funções ψ são na verdade matrizes coluna da forma

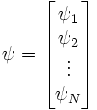
$\psi = \begin{bmatrix} \psi_1 \\ \psi_2 \\ \vdots \\ \psi_N \end{bmatrix}$

e as matrizes α₀, α₁, α₂ e α₃ devem ser hermitianas. A equação de Dirac, diferentemente da equação de Klein-Gordon, é uma equação que dá bons resultados para partículas de spin ½. Aliás, um dos sucessos é que esta equação incorpora o spin de forma natural, o que não ocorre com a equação de Schrondinger, onde o spin é admitido posteriormente como uma hipótese "ad hoc". Não obstante, isso levou a certos autores a afirmarem que o spin é um grau de liberdade relativístico, o que é contestado. Outro sucesso da equação de Dirac foi que previu a existencia do pósitron, já que a equação previa valores negativos de energia, o que foi inicialmente interpretado, à luz da “teoria dos buracos”, como indicação de elétrons com energias negativas. Essa teoria afirmava que os pósitrons seriam vacâncias produzidas pela promoção desses elétrons para estados com energias positivas. O vácuo é então visto como um “mar de elétrons”, onde eles estariam compactamente colocados. Hoje, entretanto, essa teoria cedeu lugar à questão de criação e aniquilação de partículas num contexto mais geral da quantização canônica dos campos.

Desenvolvimento da teoria quântica dos campos

A origem da teoria quântica dos campos é marcada pelos estudos de Max Born e Pascual Jordan em 1925 sobre o problema da computação da potência irradiada de um átomo em uma transição energética.

Em 1926, Born, Jordan e Werner Heisenberg formularam a teoria quântica do campo eletromagnético desprezando tanto a polarização como a presença de fontes, levando ao que se chama hoje uma teoria do campo livre. Para tanto, usaram o procedimento da quantização canônica.

Três razões principais motivaram o desenvolvimento da teoria quântica dos campos:

A necessidade da uma teoria que lidasse com a variação do número de partículas; A necessidade de conciliação entre as duas teorias: Mecânica Quântica e a relatividade; A necessidade de lidar com estatísticas de sistemas multipartículas.

Quantização canônica dos campos

Um campo, no esquema conceitual da teoria dos campos, é uma entidade com infinitos graus de liberdade. O estado de mais baixa energia, chamado de vácuo, corresponde à ausência de partículas. Estas, entretanto, podem ser criadas ou destruidas através de dois operadores:

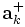$\mathbf{a}^{+}_k$

operador criação

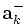$\mathbf{a}^{-}_k$

operador aniquilação

que agem sobre a função de onda do campo, respectivamente simbolizando a criação e a aniquilação de partículas dotadas de momento 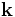$\mathbf{k}$ , possibilidade exigida pela relatividade. Os operadores, agindo sobre os estados de um tipo específico de espaço de Hilbert, chamado espaço de Fock, criam e destroem as partículas. Entretanto, uma restrição é:

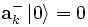
$\mathbf{a}^{-}_k\left|0\right\rangle = 0$

o que quer dizer que não pode haver aniquilação sobre o estado básico, já que nesse caso não há partículas a serem aniquiladas.

Origem: Wikipédia, a enciclopédia livre.