O que é a
A Mecânica Quântica é a parte da Física (mais particularmente, da Física moderna) que estuda o movimento das partículas muito pequenas. O conceito de partícula "muito pequena" , mesmo que de limites muito imprecisos, relaciona-se com as dimensões nas quais começam-se a notar efeitos como a impossibilidade de conhecer com infinita acuidade e ao mesmo tempo a posição e a velocidade de uma partícula (veja Princípio da incerteza de Heisenberg), entre outras. A ditos efeitos chama-se "efeitos quânticos". Assim, a Mecânica Quântica é a que descreve o movimento de sistemas nos quais os efeitos quânticos são relevantes. Experimentos mostram que estes são relevantes em escalas de até 1000 átomos. Entretanto, existem situações onde mesmo em escalas macroscópicas, os efeitos quânticos se fazem sentir de forma manifestamente clara, como nos casos da supercondutividade e da superfluidez A escala que regula em geral a manifestação dos efeitos quânticos é o raio de Bohr.
Princípios da
Para cada sistema físico é associado um espaço de Hilbert εH. O estado do sistema é definido em cada instante por um vetor normado 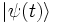 de εH.
de εH.
a) Para toda grandeza Física A é associado um operador linear auto-adjunto  pertencente a A:  é o observavel representando a grandeza A.
b) Seja 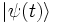 o estado no qual o sistema se encontra no momento onde efetuamos a medida de A. Qualquer que seja
o estado no qual o sistema se encontra no momento onde efetuamos a medida de A. Qualquer que seja 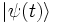 , os unicos resultados possiveis são os autovalores de aα do observavel Â.
, os unicos resultados possiveis são os autovalores de aα do observavel Â.
c) Sendo 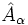 o projetor sobre o subespaço associado ao valor proprio aα, a probablidade de encontrar o valor aα em uma medida de A é:
o projetor sobre o subespaço associado ao valor proprio aα, a probablidade de encontrar o valor aα em uma medida de A é:
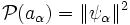 onde
onde 
d) Imediatamente após um medida de A, que resultou no valor aα, o novo estado 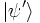 do sistema é
do sistema é
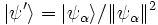
Seja 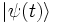 o estado de um sistema ao instante t. Se o sistema não é submetido a nenhuma observação, sua evolução ao longo do tempo é regido pela equação de Schrödinger:
o estado de um sistema ao instante t. Se o sistema não é submetido a nenhuma observação, sua evolução ao longo do tempo é regido pela equação de Schrödinger:
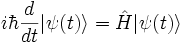
onde  é o observavel energia, ou hamiltoneana do sistema.
é o observavel energia, ou hamiltoneana do sistema.
Conclusões da
As conclusões mais importantes desta teoria são:
Em estados ligados, como o elétron girando ao redor de um átomo, a energia não se troca de modo contínuo, mas sim em de modo discreto (descontínuo), em transições cujas energias podem ou não ser iguais umas às outras. A idéia de que estados ligados têm níveis de energias discretas é devida a Max Planck.
O de ser impossível atribuir ao mesmo tempo uma posição e uma velocidade exatas a uma partícula, renunciando-se assim ao conceito de trajetória, vital em Mecânica Clássica. Ao invés da trajetória, o movimento de partículas em Mecânica Quântica é descrito por meio de uma função de onda, que é uma função da posição da partícula e do tempo. A função de onda é interpretada por Max Born como uma medida da probabilidade de se encontrar a partícula em determinada posição e em determinado tempo. Esta interpretação é a mais aceita pelos físicos hoje, no conjunto de atribuições da Mecânica Quântica regulamentados pela Escola de Copenhagen. Para descrever a dinâmica de um sistema quântico deve-se, portanto, achar sua função de onda, e para este efeito usam-se as equações de movimento, propostas por Werner Heisenberg e Erwin Schrödinger independentemente.
Apesar de ter sua estrutura formal basicamente pronta desde a década de 1930, a interpretação da Mecânica Quântica foi objeto de estudos por várias décadas. O principal é o problema da medida em Mecânica Quântica e sua relação com a não-localidade e causalidade. Já em 1935, Einstein, Podolski e Rosen publicaram seu Gedankenexperiment, mostrando uma aparente contradição entre localidade e o processo de Medida em Mecânica Quântica. Nos anos 60 J. S. Bell publicou uma série de relações que seriam respeitadas caso a localidade — ou pelo menos como a entendemos classicamente — ainda persistisse em sistemas quânticos. Tais condições são chamadas desigualdades de Bell e foram testadas experimentalmente por A. Aspect, P. Grangier, J. Dalibard em favor da Mecânica Quântica. Como seria de se esperar, tal interpretação ainda causa desconforto entre vários físicos, mas a grande parte da comunidade aceita que estados correlacionados podem violar causalidade desta forma.
Tal revisão radical do nosso conceito de realidade foi fundamentada em explicações teóricas brilhantes para resultados experimentais que não podiam ser descritos pela teoria Clássica, que incluem:
Espectro de Radiação do Corpo negro, resolvido por Max Planck com a proposição da quantização da energia. Explicação do experimento da dupla fenda, no qual elétrons produzem um padrão de interferência condizente com o comportamento ondular. Explicação por Albert Einstein do efeito fotoelétrico descoberto por Heinrich Rudolf Hertz, onde propõe que a luz também se propaga em quanta (pacotes de energia definida), os chamados fótons. O Efeito Compton, no qual se propõe que os fótons podem se comportar como partículas, quando sua enegia for grande o bastante. A questão do calor específico de sólidos sob baixas temperaturas, cuja discrepância foi explicada pelas teorias de Einstein e de Debye, baseadas na equipartição de energia segundo a interpretação quantizada de Planck. A absorção ressonante e discreta de energia por gases, provada no experimento de Franck-Hertz quando submetidos a certos valores de diferença de potencial elétrico. A explicação da estabilidade atômica e da natureza discreta das raias espetrais, graças ao modelo do átomo de Bohr, que postulava a quantização dos níveis de energia do átomo.
O desenvolvimento formal da teoria foi obra de esforços conjuntos de muitos físicos e matemáticos da época como Erwin Schrödinger, Werner Heisenberg, Einstein, P.A.M. Dirac, Niels Bohr e John von Neumann, entre outros (de uma longa lista). Em geral, a região de origem da Mecânica Quântica pode localizar-se na Europa Central, na Alemanha e Áustria, bem como a Inglaterra, e no contexto histórico do primeiro terço do século XX. Formalismos na Mecânica Quântica
É importante ressaltar que a Mecânica Quântica, assim como acontece com a mecânica clássica, pode ser apresentada de formas diferentes.
A mecânica clássica, por exemplo, pode ser descrita na linguagem das forças, que é a forma mais antiga, devida à Newton. Foi muito bem sucedida na explicação de vários fenômenos.
Mais tarde, o formalismo lagrangeano, onde o conceito mais importante não é a força, mas a energia e ação, sendo que esta última é definida em termos da energia potencial e da energia cinética.
Depois, o formalismo hamiltoniano, baseado formalmente na lagrangiana, mas com desenvolvimento matemático muitas vezes mais fácil.
Fonte: Wikipédia