A pressão é uma grandeza física que descreve a força exercida sobre uma superfície por unidade de área. Imagine que você está de pé sobre o chão: seu peso aplica uma força para baixo, e essa força está distribuída sobre a área de seus pés. A pressão nos ajuda a entender como essa força é distribuída.
Matematicamente, a pressão (\(p\)) é definida como a força (\(F\)) aplicada perpendicularmente a uma superfície dividida pela área (\(A\)) dessa superfície:
\( p = \frac{F}{A} \)
No Sistema Internacional de Unidades (SI), a pressão é medida em pascals (Pa), onde \(1 \, \text{Pa} = 1 \, \text{N/m}^2\). Isso significa que um pascal é a pressão exercida por uma força de um newton atuando uniformemente sobre uma área de um metro quadrado.
Aqui estão algumas outras unidades de pressão e suas relações com o pascal:
Essas unidades são frequentemente usadas em diferentes contextos. Por exemplo, a pressão atmosférica é geralmente medida em atmosferas (atm) ou milímetros de mercúrio (mmHg), enquanto a pressão em pneus de carro é frequentemente medida em libras por polegada quadrada (psi).
Um exemplo prático: considere uma pessoa de 70 kg de pé sobre uma superfície plana. Se a área de contato dos pés com o chão for de \(0,05 \, \text{m}^2\), a pressão exercida pela pessoa no chão pode ser calculada da seguinte maneira:
\( F = m \cdot g = 70 \, \text{kg} \cdot 9,8 \, \text{m/s}^2 = 686 \, \text{N} \)
\( p = \frac{F}{A} = \frac{686 \, \text{N}}{0,05 \, \text{m}^2} = 13.720 \, \text{Pa} \)
Portanto, a pressão exercida pela pessoa no chão é de 13.720 pascals.
Entender a pressão é crucial em diversas áreas da ciência e da engenharia, pois influencia desde o funcionamento de motores até a previsão do tempo.
O conceito de pressão nos permite entender muitos dos fenômenos físicos que nos rodeiam. Por exemplo, para cortar um pedaço de pão, utilizamos o lado afiado da faca (menor área), pois, para uma mesma força, quanto menor a área, maior a pressão produzida.

Exemplo:
Compare a pressão exercida, sobre o solo, por uma pessoa com massa de 80 kg, apoiada na ponta de um único pé, com a pressão produzida por um elefante, de 2.000 kg de massa, apoiado nas quatro patas. Considere de 10 cm² a área de contato da ponta do pé da pessoa, e de 400 cm² a área de contato de cada pata do elefante. Considere também \(g = 10 \, \text{m/s}^2\).
Resolução
A pressão exercida pela pessoa no solo é dada pelo seu peso, dividido pela área da ponta do pé:
\( p_{\text{pessoa}} = \frac{mg}{A} = \frac{80 \cdot 10}{10 \cdot 10^{-4}} = 8 \cdot 10^5 \, \text{N/m}^2 \)
A pressão exercida pelo elefante é dada por:
\( p_{\text{elefante}} = \frac{mg}{4A} = \frac{2.000 \cdot 10}{4 \cdot 400 \cdot 10^{-4}} = 1,25 \cdot 10^5 \, \text{N/m}^2 \)
Comparando as duas pressões, temos que a pressão exercida pela pessoa é 6,4 vezes a pressão exercida pelo elefante.
Exercícios
Problema 1
Aplica-se uma força de intensidade 10 N perpendicularmente sobre uma superfície quadrada de área \(0,5 \, \text{m}^2\). Qual deverá ser a pressão exercida sobre a superfície?
(A) \(5 \, \text{N.m}^2\)
(B) \(5 \, \text{N/m}^2\)
(C) \(20 \, \text{N/m}^2\)
(D) \(10 \, \text{N/m}^2\)
(E) n.d.a.
Problema 2
Um tijolo de peso 32 N tem dimensões \(16 \, \text{cm} \times 8,0 \, \text{cm} \times 4,0 \, \text{cm}\). Quando apoiado em sua face de menor área, a pressão que ele exerce na superfície de apoio é, em N/cm²:
(A) 4,0
(B) 2,5
(C) 2,0
(D) 1,0
(E) 0,50
Problema 3
Uma caixa de 500 N tem faces retangulares e suas arestas medem 1,0 m, 2,0 m e 3,0 m. Qual a pressão que a caixa exerce quando apoiada com sua face menor sobre uma superfície horizontal?
(A) \(100 \, \text{N/m}^2\)
(B) \(125 \, \text{N/m}^2\)
(C) \(167 \, \text{N/m}^2\)
(D) \(250 \, \text{N/m}^2\)
(E) \(500 \, \text{N/m}^2\)
Problema 4
O salto de um sapato masculino em área de \(64 \, \text{cm}^2\). Supondo-se que a pessoa que o calce tenha peso igual a 512 N e que esse peso esteja distribuído apenas no salto, então a pressão média exercida no piso vale:
(A) \(120 \, \text{kN/m}^2\)
(B) \(80 \, \text{kN/m}^2\)
(C) \(60 \, \text{kN/m}^2\)
(D) \(40 \, \text{kN/m}^2\)
(E) \(20 \, \text{kN/m}^2\)
Problema 5
Uma pessoa com peso de 600 N e que calça um par de sapatos que cobrem uma área de \(0,05 \, \text{m}^2\) não consegue atravessar uma região nevada sem se afundar, porque essa região não suporta uma pressão superior a \(10.000 \, \text{N/m}^2\).
Responda:
a) Qual a pressão exercida por essa pessoa sobre a neve?
b) Qual deve ser a área mínima de cada pé de um esqui que essa pessoa deveria usar para não afundar?
6. A caixa da figura abaixo tem peso 400 N e dimensões \(a = 10 \, \text{cm}\), \(b = 20 \, \text{cm}\) e \(c = 5 \, \text{cm}\) e apoia-se em uma superfície plana horizontal.
Qual a pressão, em \(\text{N/cm}^2\), que a caixa exerce no apoio, através de sua base, em cada uma das situações propostas?
I) 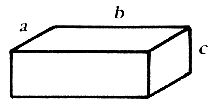
II) 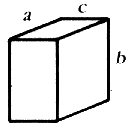
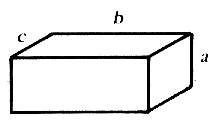
RESPOSTAS
Resolução 1
A pressão (\(P\)) é dada pela fórmula:
\( P = \frac{F}{A} \)
Substituindo os valores:
\( P = \frac{10 \, \text{N}}{0,5 \, \text{m}^2} = 20 \, \text{N/m}^2 \)
Resposta: (C) \(20 \, \text{N/m}^2\)
Resolução 2
A área da menor face é:
\( A = 8,0 \, \text{cm} \times 4,0 \, \text{cm} = 32 \, \text{cm}^2 \)
A pressão (\(P\)) é dada por:
\( P = \frac{F}{A} = \frac{32 \, \text{N}}{32 \, \text{cm}^2} = 1,0 \, \text{N/cm}^2 \)
Resposta: (D) 1,0
Resolução 3
A menor face tem área:
\( A = 1,0 \, \text{m} \times 2,0 \, \text{m} = 2,0 \, \text{m}^2 \)
A pressão (\(P\)) é dada por:
\( P = \frac{F}{A} = \frac{500 \, \text{N}}{2,0 \, \text{m}^2} = 250 \, \text{N/m}^2 \)
Resposta: (D) \(250 \, \text{N/m}^2\)
Resolução 4
Convertendo a área para \( \text{m}^2 \):
\( A = 64 \, \text{cm}^2 = 64 \times 10^{-4} \, \text{m}^2 = 0,0064 \, \text{m}^2 \)
A pressão (\(P\)) é dada por:
\( P = \frac{F}{A} = \frac{512 \, \text{N}}{0,0064 \, \text{m}^2} = 80.000 \, \text{N/m}^2 = 80 \, \text{kN/m}^2 \)
Resposta: (B) \(80 \, \text{kN/m}^2\)
Resolução 5
a) A pressão (\(P\)) exercida por essa pessoa é:
\( P = \frac{F}{A} = \frac{600 \, \text{N}}{0,05 \, \text{m}^2} = 12.000 \, \text{N/m}^2 \)
b) Para não afundar, a pressão não deve superar \(10.000 \, \text{N/m}^2\).
A área mínima (\(A_{\text{min}}\)) de cada pé de um esqui deve ser:\( A_{\text{min}} = \frac{F}{P_{\text{max}}} = \frac{600 \, \text{N}}{10.000 \, \text{N/m}^2} = 0,06 \, \text{m}^2 \)
Respostas:
a) \(12.000 \, \text{N/m}^2\)
b) \(0,06 \, \text{m}^2\)
Resolução 6
Situação I
Base: \(a \times b = 10 \, \text{cm} \times 20 \, \text{cm}\)
Área: \(A = 10 \times 20 = 200 \, \text{cm}^2\)
A pressão (\(P\)) é dada por:
\( P = \frac{F}{A} = \frac{400 \, \text{N}}{200 \, \text{cm}^2} = 2 \, \text{N/cm}^2 \)
Situação II
Base: \(a \times c = 10 \, \text{cm} \times 5 \, \text{cm}\)
Área: \(A = 10 \times 5 = 50 \, \text{cm}^2\)
A pressão (\(P\)) é dada por:
\( P = \frac{F}{A} = \frac{400 \, \text{N}}{50 \, \text{cm}^2} = 8 \, \text{N/cm}^2 \)
Situação III
Base: \(b \times c = 20 \, \text{cm} \times 5 \, \text{cm}\)
Área: \(A = 20 \times 5 = 100 \, \text{cm}^2\)
A pressão (\(P\)) é dada por:
\( P = \frac{F}{A} = \frac{400 \, \text{N}}{100 \, \text{cm}^2} = 4 \, \text{N/cm}^2 \)
Resumo das Pressões
Situação I: \(2 \, \text{N/cm}^2\)
Situação II: \(8 \, \text{N/cm}^2\)
Situação III: \(4 \, \text{N/cm}^2\)