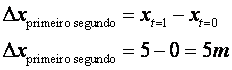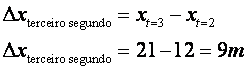Em MRUV, uma partícula se desloca 7 m durante o 2º segundo de movimento. Calcular o deslocamento, em metros, durante o 3º segundo de movimento.
A equação horária do MRUV é:
$$ \begin{align} \unicode[Garamond]{x2206}\text{x}& =\text{v}_{\text{o}}\unicode[Garamond]{x2206}\text{t} + \frac {1}{2}\text{a}\unicode[Garamond]{x2206}\text{t}^2\\ \text{se } \text{t}_{\text{o}}&=0:\\ \unicode[Garamond]{x2206}\text{x}& =\text{v}_{\text{o}}\text{t} + \frac {1}{2}\text{a}\text{t}^2\\ \text{x}& = \text{x}_{\text{o}} + \text{v}_{\text{o}}\text{t} + \frac {1}{2}\text{a}\text{t}^2\\ \text{se } \text{x}_{\text{o}}&=0:\\ \text{x}& = \text{v}_{\text{o}}\text{t} + \frac {1}{2}\text{a}\text{t}^2\\ \end{align} $$Vamos analisar os dados fornecidos no enunciado.
A velocidade em t=1s é:
$$ \begin{align} \text{v}_{\text{t=1}}&= \text{v}_{\text{t=0}}.\unicode[Garamond]{x2206}\text{t}+\text{a}\text{t}\\ \text{v}_{\text{t=1}}&= 0.1+\text{a}.1\\ \text{v}_{\text{t=1}}&= \text{a}\\ \end{align} $$A velocidade em t=2s é:
$$ \begin{align} \text{v}_{\text{t=2}}&= \text{v}_{\text{t=1}}.\text{t}+\text{a}\text{t}\\ \end{align} $$sabendo que \( \text{v}_{\text{t=1}}= \text{a} \) chegamos a:
$$ \begin{align} \text{v}_{\text{t=2}}&= a + a.2\\ \text{v}_{\text{t=2}}&= \text{a} + \text{a} \\ \text{v}_{\text{t=2}}&= 3\text{a} \\ \end{align} $$em t=3s teremos:
$$ \begin{align} \text{v}_{\text{t=3}}&= \overbrace {\text{a}}^{\text{v}_{\text{t=2}}}. \overbrace {1}^{ \unicode[Garamond]{x2206}\text{t}} + \text{{a}}.\overbrace {1}^{ \unicode[Garamond]{x2206}\text{t}} \\ \text{v}_{\text{t=3}}&= 3\text{a} + \text{a} \\ \text{v}_{\text{t=3}}&= 4\text{a} \\ \end{align} $$Até este momento do cálculo já sabemos que:
$$ \begin{array} {|r|r|r|} \hline t(s) & 0 & 1 & 2 & 3 \\ \hline x(m) & 0 & - & - & - \\ \hline v(m) & 0 & 2a & 3a & 4a \\ \hline \end{array} $$Durante o 1o segundo, ou seja, emtre t=0s e t=1s sabemos que:
$$\begin{align} \unicode[Garamond]{x2206}\text{x}& =\text{v}_{\text{o}}\unicode[Garamond]{x2206}\text{t} + \frac {1}{2}\text{a}\unicode[Garamond]{x2206}\text{t}^2\\ \unicode[Garamond]{x2206}\text{x}& =\text{v}_{\text{t=1}}\unicode[Garamond]{x2206}\text{t} + \frac {1}{2}\text{a}\unicode[Garamond]{x2206}\text{t}^2\\ x &= 2a.1 + 1/2.a.1^2\\ x &= 2a + 1/2.a\\ x &= 3/2a\\ \end{align} $$
E nossa tabela ganha mais um valor:
$$ \begin{array} {|r|r|r|} \hline t(s) & 0 & 1 & 2 & 3 \\ \hline x(m) & 0 & 3/2a & - & - \\ \hline v(m) & 0 & 2a & 3a & 4a \\ \hline \end{array} $$Durante o 2o segundo, ou seja, emtre t=1s e t=2s sabemos que:
$$\begin{align} \unicode[Garamond]{x2206}\text{x}& =\text{v}_{\text{o}}\unicode[Garamond]{x2206}\text{t} + \frac {1}{2}\text{a}\unicode[Garamond]{x2206}\text{t}^2\\ \unicode[Garamond]{x2206}\text{x}& =\text{v}_{\text{t=1}}\unicode[Garamond]{x2206}\text{t} + \frac {1}{2}\text{a}\unicode[Garamond]{x2206}\text{t}^2\\ 7 &= 2a.1 + 1/2.a.1^2\\ 7 &= 2a + 1/2.a\\ 7 &= 5/2.a\\ a &=14/5 m/s2 \end{align} $$
e a tabela ganha um aspecto mais nítido
$$ \begin{array} {|r|r|r|} \hline t(s) & 0 & 1 & 2 & 3 \\ \hline x(m) & 0 & 3/2a\to 3/2\times14/5\to 42/10\to4,2 & - & - \\ \hline v(m) & 0 & 2a & 3a & 4a \\ \hline \end{array} $$
0s até 1s
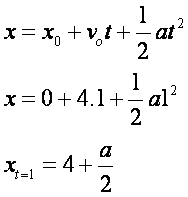
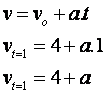
(essa é a rapidez no instante t=1s)
1s até 2s
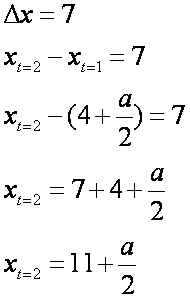
Deslocamento DURANTE o 2º segundo
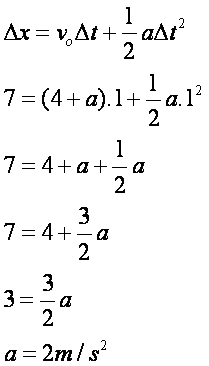
Agora temos TODAS as informações, com isso podemos montar a equação horária:
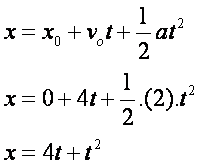
Logo, podemos montar uma tabela ![]()
t(s) |
0 |
1 |
2 |
3 |
4 |
x(m) |
0 |
5 |
12 |
21 |
32 |
Agora só resta calcular os deslocamentos: