Dos postulados da teoria da relatividade resulta um conjunto de importantes corolários que afetam as propriedades do espaço e do tempo. Nós não nos deteremos na explicação relativamente difícil destes corolários. Limitemo-nos a enumerá-los.
A distância não é uma grandeza absoluta, mas depende do movimento do corpo em relação a um dado sistema de referência.
Designemos por $\ell_o$ o comprimento de uma vara no sistema de referência K, em relação ao qual a vara está parada. Então o comprimento $\ell$ , desta vara, no sistema $\mathtt {K_1}$ , em relação ao qual a vara se move com velocidade v, determina-se pela fórmula.
$\mathtt{\ell=\ell_o \sqrt{1-\frac{v^2}{c^2}}}$ (1)
Como se vê por esta fórmula ,
$(\ell < \ell_o)$
Nisto consiste a redução relativista do corpo nos sistemas de referência em movimento.
Seja o intervalo de tempo entre dois acontecimentos que se dão no mesmo ponto do sistema inercial K igual a $\tau_o$ . Tais acontecimentos podem ser, por exemplo, dois batimentos de um metrônomo que conta os segundos.
Então o intervalo $\tau$ entre estes acontecimentos, num sistema de referência $\mathtt {K_1}$, que se move em relação ao sistema $\mathtt {K}$ com a velocidade $\mathtt {v}$, exprime-se do seguinte modo.
$\mathtt {\tau=\frac{\tau_o}{\sqrt{1-\frac{v^2}{c^2}}}}$ (2)
Evidentemente $\tau > \tau_o$ . Trata-se do efeito relativista de atraso do tempo nos sistemas de referência em movimento.
Se tivermos $\mathtt {v\ll c }$ , nas fórmulas (1) e (2) pode desprezar-se a grandeza $\mathtt {\frac{v^2}{c^2}}$. Então será
$\ell \approx \ell_o$ e $\tau \approx \tau_o$
ou seja, a redução dos corpos e o atraso do tempo relativistas num sistema de referência em movimento podem não ser tomados em consideração.
A lei relativista da composição das velocidades. Aos novos conceitos relativistas de espaço e de tempo corresponde uma nova lei da composição das velocidades. Evidentemente que a lei clássica da composição das velocidades não pode ser verdadeira, visto que ela contradiz a afirmação de que a velocidade da luz é constante na vácuo.
Se um comboio se move com a velocidade $\mathtt {v}$ e num vagão, segundo a direção do movimento do comboio, se propaga uma onda luminosa, então a sua velocidade em relação á Terra deve ser igual de novo a $\mathtt {c}$ , e não a $\mathtt {v+c}$. A nova lei da composição das velocidades deve conduzir ao resultado pretendido.
Formularemos a lei da composição das velocidades para o caso particular em que o corpo se movimenta ao longo do eixo $\mathtt {X_1}$ do sistema de referência K1 , o qual, por sua vez, se move com a velocidade $\mathtt {v}$ em relação ao sistema de referência K. Além disso, os eixos das coordenadas $\mathtt {X}$ e $\mathtt {X_1}$ coincidem sempre, enquanto os eixos das coordenadas Y e Y1 , $\mathtt {Z}$ e $\mathtt {Z_1}$ se mantêm paralelos (fig. 4) .
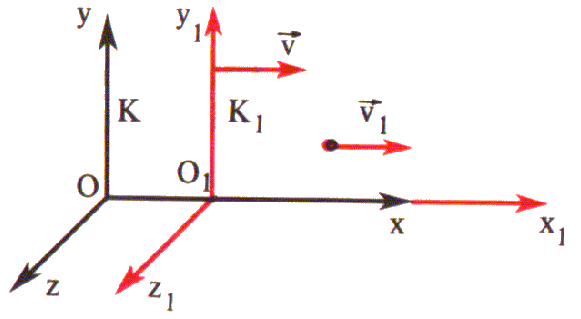
Fig. 4
Representemos a velocidade do corpo em relação a $\mathtt {K_1}$ por $\mathtt {v_1}$, a velocidade do mesmo corpo em relação a $\mathtt {K}$ por $\mathtt {v_2}$. Então, de acordo com a lei relativista da composição de velocidades,
$\mathtt {v_2=\frac{v_1+v}{1+\frac{v_1v}{c^2}}}$
Se $ \mathtt {v\ll c }$ e $\mathtt { v_1\ll c }$ , então podemos desprezar o termo $\mathtt {\frac{v_1v}{c^2}}$ no denominador e, em vez de (3) , obtermos a lei clássica da composição das velocidades:
$\mathtt {\vec V_2 = \vec V_1 + \vec V}$
Quando $\mathtt {v_1=c}$ , a velocidade $\mathtt {v_2}$ também se torna igual a $\mathtt {c}$ , tal como exige o segundo postulado da teoria da relatividade . De fato,
$\mathtt {v_2 = \frac {c + v}{1 + \frac{cv}{c^2}} = c \frac {c+v}{c+v}=c}$
Uma admirável propriedade da lei relativista da composição de velocidades consiste em que, para quaisquer velocidades $\mathtt {v_1}$ e $\mathtt {v}$ (evidentemente, não superiores a c ) a velocidade $\mathtt {v_2}$ não é superior a c . No caso limite em que $\mathtt {v_1=v=c}$ obtém-se
$\mathtt {v_2=\frac{2c}{c}=c}$
A velocidade $\mathtt {v>c}$ não é possível. A esta conclusão também se pode chegar através de raciocínios formais. De fato, se $\mathtt {v>c}$ , as fórmulas (1) e (2) perdem o significado, visto que o comprimento e o tempo se tornam imaginários.