RELATIVIDADE

INTRODUÇÃO À RELATIVIDADE RESTRITA

5. Dependência da Massa em Relação à Velocidade: Dinâmica Relativista

"A massa, que desde o tempo de Newton, durante dois séculos e meio, se considerava invariável, na realidade depende da velocidade."

No caso de grandes velocidades, as leis da mecânica de Newton não estão de acordo com os novos conceitos de espaço e de tempo. Só quando a velocidade é pequena e os conceitos clássicos de espaço e de tempo são válidos, a Segunda Lei de Newton

$$\mathtt {m \frac { \Delta \vec v }{ \Delta t } = \vec F ~~~~~(4)}$$

não se altera com a transição de um sistema de referência inercial para outro (verifica-se o princípio da relatividade).

Para a velocidades grandes, porém, esta lei, na sua forma habitual (clássica), não é verdadeira.

De acor do com a Segunda Lei de Newton (4) uma força constante, que atue no corpo durante algum tempo, pode transmitir-lhe uma velocidade tão grande quanto se queira. Mas na realidade, a velocidade da luz no vácuo é limitada, e em nenhumas condições um corpo pode mover-se com uma velocidade maior do que a velocidade da luz no vácuo. É necessária uma pequena mudança na equação do movimento dos corpos para que ela se torne verdadeira para grandes velocidades do movimento. Passemos previamente à formulação da segunda lei da dinâmica, utilizada pelo próprio Newton:

$$\mathtt {m \frac { \Delta \vec v }{ \Delta t } = \vec F ~~~~~(5)}$$

onde

$$\mathtt {\vec p = m\vec v}$$ é o impulso (quantidade de movimento) do corpo. Nesta equação, a massa do corpo considerava-se independente da velocidade.

É surpreendente que mesmo no caso de grandes velocidades a equação (5) não muda de forma. As modificações só dizem respeito à massa. Quando aumenta a velocidade do corpo a sua massa não se mantém constante, mas aumenta. O aumento da massa é tanto mais acentuado quanto mais perto a velocidade do corpo estiver da velocidade da luz \( \mathtt {c} \),

A dependência da massa em relação à velocidade pode calcular-se a partir da suposição de que a lei da conservação do impulso é verdadeira para as novas concepções de espaço e de tempo. Os cálculos são demasiado complicados. Apresentemos apenas os resultados finais.

Fig. 5

Fig. 5

Se designarmos através de \( \mathtt {m_o} \) a massa do corpo em repouso, então a massa \( \mathtt {m} \) deste mesmo corpo em movimento com velocidade \( \mathtt {v} \) define-se pela equação:

$$\mathtt {m=\frac{m_o}{\sqrt{1-\frac{v^2}{c^2}}}~~~~~(6)}$$

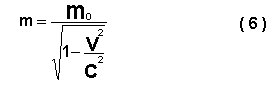
Na figura (5) está representada a dependência da massa do corpo em relação à sua velocidade.

Quando a velocidade do movimento é muito menor do que a da luz, a expressão: $$\mathtt {\sqrt{1-\frac{v^2}{c^2}}} $$

pouco difere da unidade. Assim, para a velocidade de uma nave espacial atual, \( \mathtt{v\gg 10km/s} \), obtemos:

$$\mathtt {\sqrt{1-\frac{v^2}{c^2}} = 0,999 999 999 44} $$

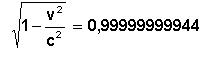
Não é de admirar, por isso, que não se note o aumento da massa com o aumento da velocidade quando comparamos pequenas velocidades. Mas as partículas elementares, nos atuais aceleradores de partículas carregadas, atingem velocidades enormes. Se a velocidade de uma partícula for apenas 90 km/s menor do que a velocidade da luz, então a sua massa aumenta 40 vezes. Os aceleradores potentes de elétrons podem imprimir a estas partículas velocidades inferiores à velocidade da luz apenas em 35 - 40 m/s. Nestas condições, a massa do elétron aumenta aproximadamente 2000 vezes e torna-se maior que a do próton. para que este elétron se mantenha numa órbita circular é necessário que o campo magnético exerça sobre ele uma força 2000 vezes maior do que se poderia supor, não considerando a dependência de massa em relação à velocidade. Para calcular a trajetória de partículas rápidas já não se pode utilizar a mecânica de Newton.

De acordo com a relação (6) , o impulso de um corpo é igual a:

$$\mathtt {\vec p=\frac{m_o \vec v}{\sqrt{1-\frac{v^2}{c^2}}}~~~~~(7)}$$

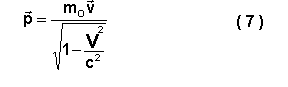
A lei fundamental da dinâmica relativista mantém a forma anterior

$$\mathtt { \frac { \Delta \vec p }{ \Delta t } = \vec F}$$

No entanto, o impulso do corpo neste caso define-se pela equação (7), e, não pelo simples produto \( \mathtt { m_o \vec v } \) .

Deste modo, a massa, que desde o tempo de Newton, durante dois séculos e meio, se considerava invariável, na realidade depende da velocidade.

À medida que aumenta a velocidade, a massa do corpo, definida pelas suas propriedades inerciais, aumenta. Quando \( \mathtt {v \to c}\) , a massa do corpo, de acordo com a equação (6) cresce ilimitadamente \(( \mathtt {m \to \infty})\) ; por isso, a aceleração tenda para zero, e a velocidade praticamente deixa de aumentar, por mais que se prolongue a ação da força.

A necessidade de utilizar a equação do movimento relativista, quando se calcula a aceleração de partículas carregadas, significa que a teoria da relatividade, no nosso tempo, passou a ser uma ciência estreitamente ligada à engenharia.

As leis da mecânica de Newton podem ser consideradas um caso particular da mecânica relativista, sendo verdadeiras quando a velocidade do movimento do corpo é muito menor do que a velocidade da luz.